What’s formal verification?
I recently learned about software formal verification tools like TLA+ and Alloy. These tools are magical - they let you model your distributed system as a state machine and verify that conditions you define, known as invariants, are satisfied in all possible states.
Questions like:
What if our database write fails here?
What if we can't get the lock on this shared resource?
What if I get hit by a bus on the way to work tomorrow?
What if this asynchronous operation finishes before another one?
and more can be defined by modelling and verifying your software’s operations exhaustively.
Ok cool, what’s a model and how do I make one?
Tools like Alloy require a model. A model is some representation of your system’s states, data, state transitions, and invariants. Let’s start with a simple example and eventually use Alloy to verify it. We prefer to use Alloy here to demonstrate a higher-level use-case. TLA+ is much more verbose and less intuitive, based on its origins in mathematics.
Say that your side-hustle is selling personalized knitted sweaters. You make a website where anyone can place an order. You write some code to automate the checkout process. After a while, your customers start complaining. They report being charged despite not receiving a Sweater! To get to the bottom of this, you decide to model your software using Alloy, hoping that its verifier can tell you if there’s bugs with your software implementation.
Installing
Alloy editor/visualizer can be downloaded here.
Defining our Model’s Objects
In Alloy, we use the sig keyword to define an object that we can add logical rules around. To model this situation, we define the following objects.
// Represent money, customers (that have money), and the sweaters that they buy.
sig Money {}
sig Customer {}
sig Sweater {}
// Everytime a customer makes an action, a new state is generated.
sig State {
customers: Customer -> Money,
sweaters: Sweater -> Customer
} { }
Our State object is used to signify the state of the world. Whenever, we receive a new order, we will update the fields in State to reflect them. The customers field is mapping between customers and money, whereas the sweaters field is a mapping between sweaters and money.
Alloy supports basic polymorphism using the extends keyword. We can use it to designate a starting state which has special properties.
// Define the StartState.
sig StartState extends State {}
Spitting Facts
Now, let’s define some facts. In Alloy, a fact is a condition that we know to be true and impose on our model. Just like we know for a fact that jet fuel can’t melt steel beams.
fact {
// Each Money is assigned to a Customer in the StartState
all m: Money | one c: Customer | (c->m) in StartState.customers
// No Sweater is owned in the StartState
all s: Sweater | all c: Customer | (s->c) not in StartState.sweaters
// The StartState defines all Customer->Money mappings and they don't change.
all t: State | no(t.customers - StartState.customers)
}
The syntax here is pretty overwhelming - there’s a lot going on. First of all, Alloy’s underlying verification system is based on set theory. You can think of the earlier objects we defined to each be a set:
- So
Sig Money {}really means{m1, m2, ...}representing all possible money - and
Sig Customer {}really means{c1, c2, ...}representing all possible customers - Therefore, the
Customer -> Moneyexpression inStatedefines a mapping betweenCustomerandMoney. This would be all 2-tuples where the first value is a member ofCustomerand the second is a member ofMoney:{(c1, m1), (c2, m2), ...}
Facts impose restrictions on how these sets interacts and the possible combinations between them.
- The first condition states that for each piece of money, there is one assigned customer in the
StartState’s customer list. This prevents money from not being accounted for. - The second fact is similar and enforces that the
sweatersfield is empty inStartState. - The last fact makes use of the first fact and set difference operator (
-) to ensure that futureStatesdo not have newCustomer->Moneymappings. Since theStartStateincludes all possible mappings, if the set difference between a futureState’s customers and theStartState’s customers is empty (as indicated by thenooperator), then the original mappings are preserved.
Writing Operations using Predicates
Now, we can write predicates that define the transition between states. Alloy is declarative - not imperative. Instead of telling it how something happens, you tell it how to detect that something has happened. This allows Alloy to construct examples of possible states and generate counter examples.
pred ProcessOrder [c: Customer, m: Money, s: Sweater, t1, t2: State] {
// The Customer should have less Money in the new State.
t2.customers = t1.customers - (c->m)
// The Customer now owns the Sweater.
t2.sweaters = t1.sweaters + (s->c)
}
A predicate is a boolean function defined by the pred keyword. This predicate tells Alloy how a processed order is detected; given a Customer c with Money m, and the starting State t1, we generate the ending State t2.
Let’s add another predicate that verifies that your customers are each getting a unique sweater every time an order is processed.
// In every State, Each Sweater should be owned by at most 1 Customer
pred SweatersUniquelyOwned [t: State] {
all s: Sweater | one c: Customer | (s -> c) in t.sweaters
}
It’s finally time to invoke these predicates and see if there’s any bugs.
Checking Correctness Using Assertions
We use the assert keyword to define an assertion. This assertion makes sure that for all pairs of states where one State is the result of an order processed on the previous State, each Sweater in the final State is uniquely owned.
assert CustomerOrdersFulfilled {
all c: Customer, m: Money, s: Sweater, t1, t2: State |
ProcessOrder[c, m, s, t1, t2] => SweatersUniquelyOwned[t2]
}
check CustomerOrdersFulfilled for 1 StartState, 2 State, exactly 2 Customer, exactly 2 Money, 1 Sweater
We use the check keyword to run the assertion on a fixed problem space. Even though our models are seemingly infinite, by restricting the number of Objects we verify with, we effectively make our model finite. In practice, we would choose large object numbers to verify our models but these would take longer and be more CPU-intensive.
Surely enough, Alloy has found a counter-example!
Executing "Check CustomerOrdersFulfilled for 1 StartState, 2 State, exactly 2 Customer, exactly 2 Money, 1 Sweater"
Actual scopes: exactly 2 Money, exactly 2 Customer, 1 Sweater, 2 State, 1 StartState
Solver=sat4j Bitwidth=4 MaxSeq=4 SkolemDepth=1 Symmetry=20 Mode=batch
297 vars. 27 primary vars. 528 clauses. 5ms.
. found. Assertion is invalid. 3ms.
This is the state tree in Alloy’s counter-example:
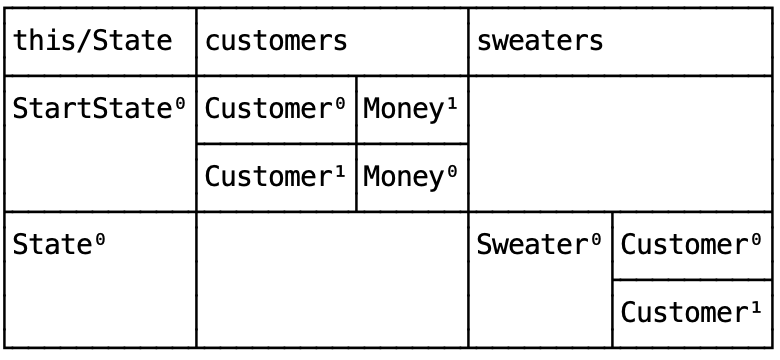
It turns out that when we were fulfilling orders, we weren’t making sure that each customer was receiving a unique sweater! In this case, both Customer0 and Customer1 placed orders in the StartState and in the next State, Sweater0 was assigned to two customers!
With this information, you fix your order processing software and send sweaters to all affected customers just in time for Christmas. You can now update your model to reflect this new logic by adding a new fact that enforces unique sweater assignments.
Final Thoughts
Alloy and other formal verification tools are really powerful, especially when the complexity of your system grows. The issue is that there’s a steep learning curve and modelling a large system accurately is really hard. This is a big reason why formal verification has not seen widespread industry adoption.
In the coming weeks, I’m going to look into how AI can help expedite model generation; it should dramatically improve the speed and accuracy of modelling complex software.